Haftanın Sorusu #23’ün cevabı

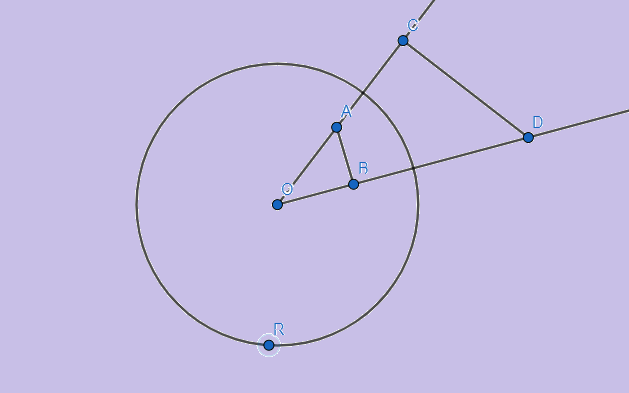
Şekilden takip edilebileceği üzere ve ise eşitliği geçerli olur. Buradan da eşitliğini çıkarabiliriz.

Demek ki merkezden geçmeyen bir doğru parçası alırsak ve üçgenleri benzer.

Şimdi merkezden geçmeyen çemberimizin uzantısı merkezden geçen çapını ele alalım. Bu çapla beraber çember üzerindeki her nokta bir dik üçgen verir.

Az önce kanıtladığımız üzere fonksiyon üçgenleri benzer üçgenlere götürüyor, bu da fonksiyonun görüntüsünün bir doğru parçasını hipotenüs kabul eden noktalar kümesi olduğunu görürüz ki bu da tam olarak bir çemberdir. (Kanıtlamayı deneyin)

Doğru cevap gönderen Musa Savari’ye ve kritik bir düzeltme yapan Berke Yavuz’a teşekkürler.