Haftanın Sorusu #22’nin cevabı

n elemanlı bir kümeden kendine giden n! eşleme vardır. Bu eşlemeler bileşke işlemi altında bir grup oluşturur. n elemanlı bir kümenin permütasyonlarından oluşan bu gruba n. simetrik grup denir ve Sym(n) olarak gösterilir.

Her sonlu grubun, bir n doğal sayısı için Sym(n)’in bir altgrubuna izomorf olduğunu gösteriniz.

Grubumuzun eleman sayısı olsun. Şimdi bir için fonksiyonuna bakalım. Bu fonksiyon birebir ve örten çünkü: eğer ve elemanları aynı yere gidiyorsa eşitliğinde tarafları soldan ile çarparak elde ederiz. Yani fonksiyon birebir. Örten olduğunu görmek içinse herhangi bir alıp fonksiyonun görüntüsünde mi diye bakalım. Hemen fark ederiz ki ‘yı fonksiyonda değerlendirince elde ediyoruz. Demek ki bir eşleme. O halde ‘in bir elemanı.

‘nin her elemanı için bunun gibi bir eşleme buluruz. fonksiyonu bir homomorfidir. (Kanıtlayınız.) Birebir olduğunu da kolayca kanıtlayabiliriz. Bir sabitleyip fonksiyonda aldığı değerlere bakalım. Az önce yaptığımız gibi sağdan ile çarparsak istediğimizi kanıtlarız.

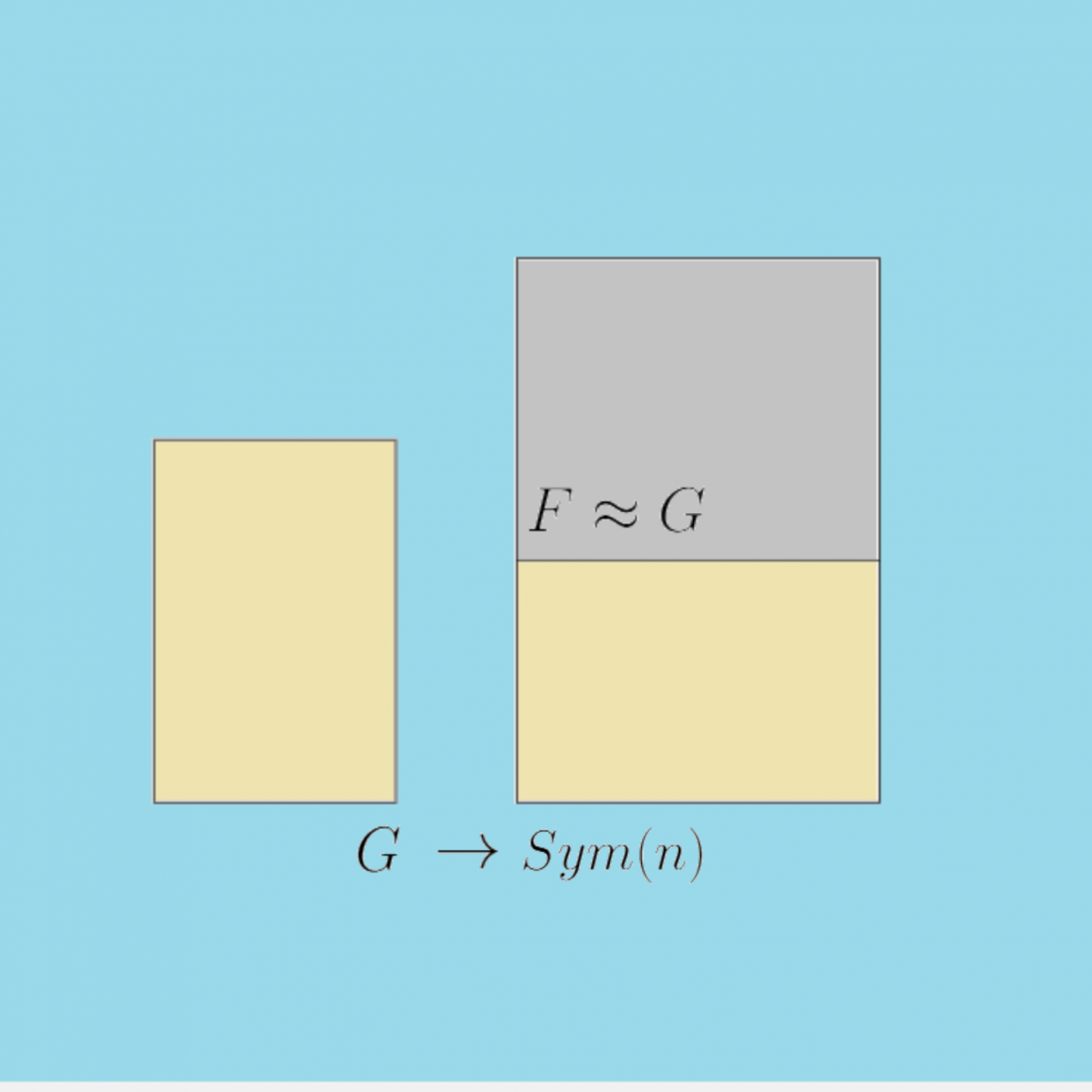
Bu homomorfinin görüntüsü bize ‘in içinde ve ‘ye izomorf bir grup verdi. Demek ki her sonlu grubu bir için elemanlı bir kümenin permütasyonları grubunun altgrubu olarak görebiliriz.

Doğru yanıt gönerenler: Musa SAVARİ